Metoda konečných prvků a její použití

Schopnost předpovídat chování strojů a zařízení má obecně má velký význam v každé fázi inženýrského procesu, ať už se jedná o návrh, výrobu nebo provoz.

Při navrhování konstrukcí a zjištění vhodnosti návrhu pro daný účel z hlediska tuhosti a pevnosti lze k řešení přistoupit třemi způsoby. Pomocí analytického řešení, pomocí numerického výpočtu a pomocí reálné zkoušky na reálné konstrukci-prototypu. Analytická řešení nejsou univerzální a lze je aplikovat pouze na jednoduché problémy. Analytická řešení jsou matematická vyjádření daného problému, která umožňují vypočítat požadovanou neznámou hodnotu, např. průhyb v jakémkoliv bodě konstrukce. Tato řešení obecně vyžadují řešení běžných nebo parciálních diferenciálních rovnic, které jsou vytvořeny inženýry, fyziky a matematiky, aby se eliminovala potřeba vytváření a testování mnoha prototypových řešení, což může být značně nákladné. V případě komplexnějších geometrií, zatížení a materiálových vlastností není možné řešení diferenciálních rovnic získat. V tomto případě zde máme numerické metody jako je např. metoda konečných prvků (FEM), pomocí které je možné aproximovat řešení diferenciálních rovnic. 

Metoda konečných prvků vznikla v oblasti strukturální mechaniky a poté byla rozšířena do dalších oblastí mechaniky těles a dále také do oblastí, jako je přenos tepla, dynamika tekutin a elektromagnetismus. Jedním z důvodů popularity MKP je to, že výsledkem metody jsou počítačové programy s univerzální povahou, které dokážou vyřešit mnoho praktických problémů. Je však nutné řádné porozumění teoretickému pozadí nejen metody konečných prvků, ale také teorii z oblasti mechanického chování těles, pružnosti a pevnosti, nauky o materiálech apod. To jak z důvodu správného nastavení výpočtu, tak kvůli zhodnocení výsledků během přípravy a ladění modelu, a v poslední řadě kvůli správné interpretaci výsledků.

Klasické analytické metody uvažují diferenciální element a vyvíjí řídící rovnice obvykle ve formě parciálních diferenciálních rovnic. Při aplikaci na praktické problémy, které se vyznačují složitou geometrií a okrajovými podmínkami, je složité  respektive  nemožné získat exaktní řešení těchto rovnic. Metodu konečných prvků lze tedy zjednodušeně chápat jako metodu, která pomáhá nalézt aproximované (přibližné) řešení parciálních diferenciálních rovnic nebo jako nástroj pro transformaci parciálních diferenciálních rovnic na algebraické rovnice, které lze snadno vyřešit.

Klíčové body metody konečných prvků lze shrnout následovně:

• Jelikož řešení splňující jak okrajové podmínky, tak diferenciální rovnici není známo zavádí se tzv. zkušební řešení, které je voleno tak, aby byly splněny okrajové podmínky.
• Předpokládané zkušební řešení obecně nesplňuje diferenciální rovnici přesně a ponechává určité residuum, tj. chybu řešení diferenciální rovnice.
• Residuum se obecně liší bod od bodu skrze řešenou doménu a nelze ho všude vynulovat. Lze ho vynulovat na vybraných místech domény, ale přednost je dávána tomu, aby byl zbytek ve všech bodech co nejmenší.
• Pro složité komplexní problémy reálného světa je volba jedné spojité zkušební funkce, která bude platná skrze celou doménu a bude splňovat okrajové podmínky, velmi složité. Proto se doména raději diskretizuje (rozděluje) na několik částí (konečných prvků) a je použito několik zkušebních funkcí, každá platná pro určitý konečný prvek.
• Zkušební funkce použité v každém konečném prvku jsou známe jako tzv. tvarové funkce elementů. Tyto funkce jsou definovány ve formě interpolačních funkcí, které jsou použity k interpolaci hodnoty proměnné uvnitř prvku z hodnot v bodech nazývaných uzly. Typické konečné prvky používané při analýze pomocí metody konečných prvků jsou zobrazeny na obr.
• Pro každý tvar prvku jsou odvozené charakteristické matice, které jsou předem programovány do softwarů jako jsou Nastran, Ansys apod. Diskretizace domény záleží na uživateli, který si může zvolit z různých prvků. Počítačový program nastaví charakteristické matice pro jednotlivé zvolené prvky a z elementárních matic sestaví jednu globální matici celého systému, ze které vzejde konečné řešení.

Názorný příklad:

Použití metody konečných prvků a rozdíl ve výsledcích v porovnání s analytickým výpočtem, si ukážeme na příkladu jednoduchého vetknutého nosníku. 

Vetknutý nosník je zatížen na volném konci silou F. Jak velký bude ohyb a natočení volného konce? Výpočet proveden na nosníku IPE 80, délka nosníku L = 1 m a síla F = 1000 N. Materiál nosníku je ocel S235, modul pružnosti v tahu E = 210 000 MPa a Poissonův poměr µ = 0,3.

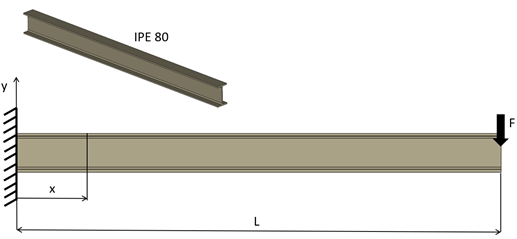
Obr. 1 Zadání příkladu

Exaktní řešení

U tohoto problému je známé exaktní řešení, které vychází z řešení diferenciální rovnice

w´´(x )= -(M(x) / EI)

Řešením difereneciální rovnice pro nosník viz zadání, dostáváme pro natočení v jakémkoliv bodě rovnici:

w´ = φ = F / 2EI(x^2-2Lx)

a pro průhyb v jakémkoliv bodě:

w = (F / 6EI) (x^3 - 3Lx^2)

Nás zajímá hodnota průhybu a natočení volného konce nosníku tj.místo kdy x = L. Dosazením L za x dostáváme pro natočení:

φL = -(FL^2 / 2EI)

a pro průhyb:

wL = -(FL^3 / 3EI)

Předpoklad je, že nosník je zatížen ve směru osy s větší ohybovou tuhostí. Dosazením síly F = 1000 N, délky nosníku L = 1000 mm, modulu pružnosti E = 210 000 MPa a kvadratického momentu průřezu I (Izz) = 801 810,7 mm4 dostáváme:

L = -(1000*1000^2 / 2*210 000*801 810,7) = -0,002969 rad = -0.17°

w=-(1000*1000^3 / 3*210 000*801 810,7) = -1,98 mm

Řešení pomocí FEM

Při řešení pomocí FEM je potřeba provézt 3 základní kroky – preprocessing tj. příprava výpočetního modelu, výpočet a v posledním kroku postprocessing tj. vyhodnocení výsledků. 

Při přípravě výpočetního modelu je důležité vytvořit model, který bude co nejvěrněji napodobovat chování skutečné konstrukce. Snahou je, detailní model, který je určený pro tvorbu výrobní dokumentace, co nejvíce zjednodušit, a to tak aby se usnadnila tvorba výpočetní sítě, ale zároveň aby to výrazně neovlivnilo chování vůči skutečné konstrukci. Mezi prvky, které se často zanedbávají patří např. sražení a zaoblení hran, svarové spoje, šroubové spoje apod. Dále se zjednodušuje samotná geometrie u prvků, u kterých je to možné. Prvky jejichž jeden rozměr výrazně přesahuje zbývající rozměry, se zjednodušují na 1D křivku. Typickým příkladem jsou nosníky, tyče a trubky. Prvky jejichž 2 rozměry jsou výrazně větší než 3. rozměr, jsou zjednodušovány na plochy a patří sem typicky tenkostěnné prvky, skořepiny a desky. 

U nosníku IPE 80 máme 3 možnosti modelování, a to pomocí – nosníkových elementů (1D), skořepinových elementů (2D) nebo tělesových elementů (3D).

Řešení pomocí 1D nosníkových elementů

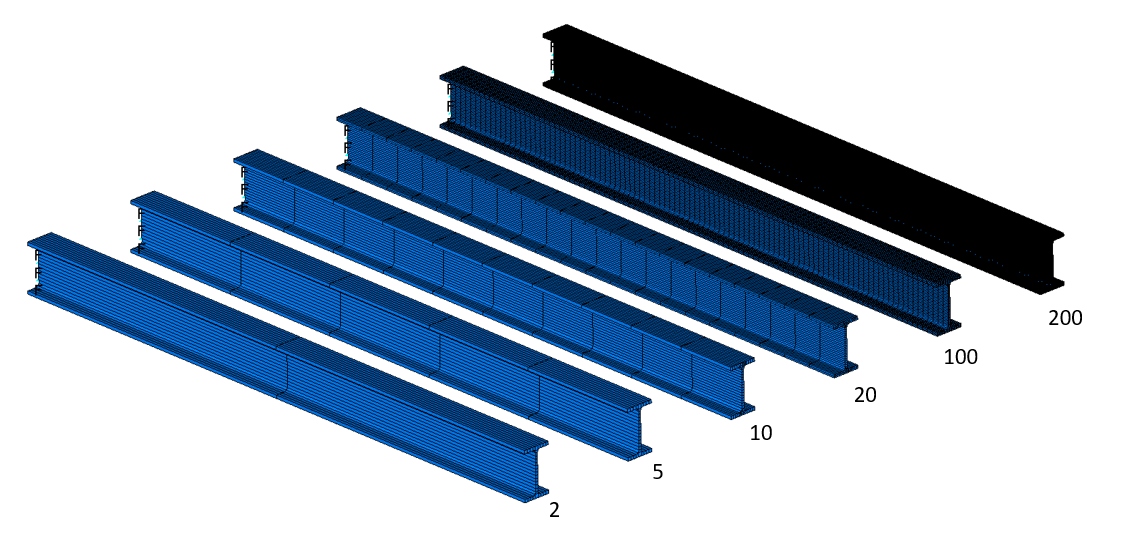
Na obr. 1 je zobrazeno 5 modelů nosníku s počtem elementů od 1 do 500. V tomto případě jsou elementy pouze čáry, v jejichž vlastnostech jsou definovány hodnoty, které charakterizují daný průřez a výpočet probíhá na základě některé ověřené hypotézy např. Euler-Bernoulliho hypotézy. 

Volba počtu elementů je čistě na výpočtáři. Počet elementů musí být určen tak, aby byl výsledek co nejpřesnější, ale zároveň aby časová náročnost výpočtu nebyla příliš velká.

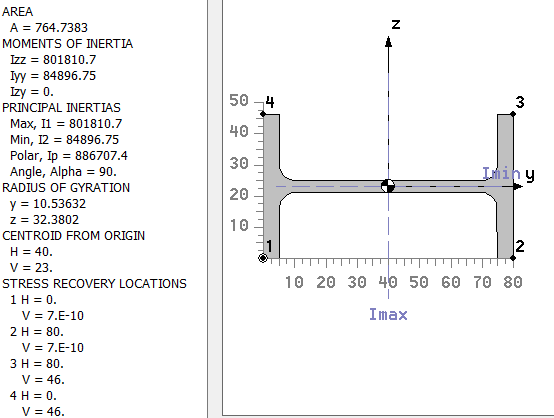
Obr. 2 Definové vlastnosti nosníkových elementů pro průřez IPE 80

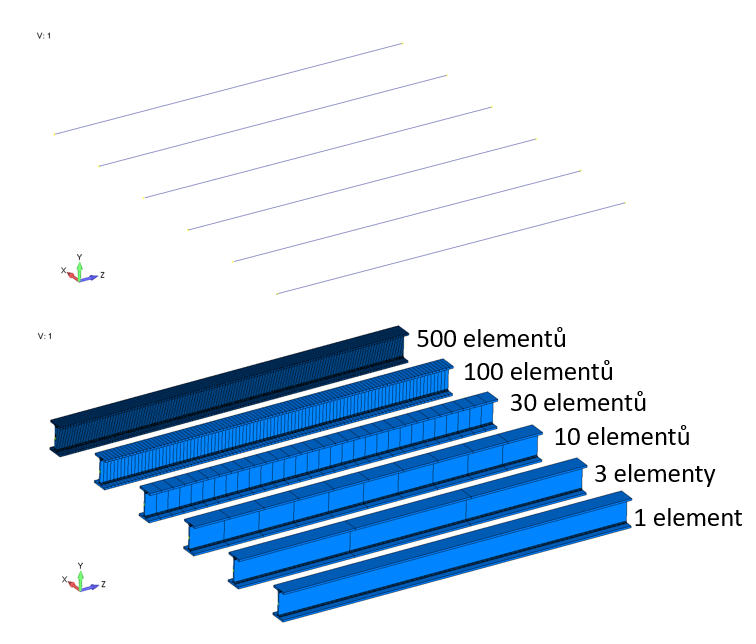
Obr. 3 Nosníky vytvořené pomocí různého počtu nosníkových elementů

Při přípravě modelu je potřeba definovat okrajové podmínky, které říkají, v jakých směrech se může nebo nemůže model pohybovat, deformovat apod. V tomto příkladě se jedná o vetknutý nosník, a proto bylo na jednom konci nosníku odebráno 6 stupňů volnosti – 3 translační a 3 rotační. Na druhém konci byla definována síla F = 1000 N.

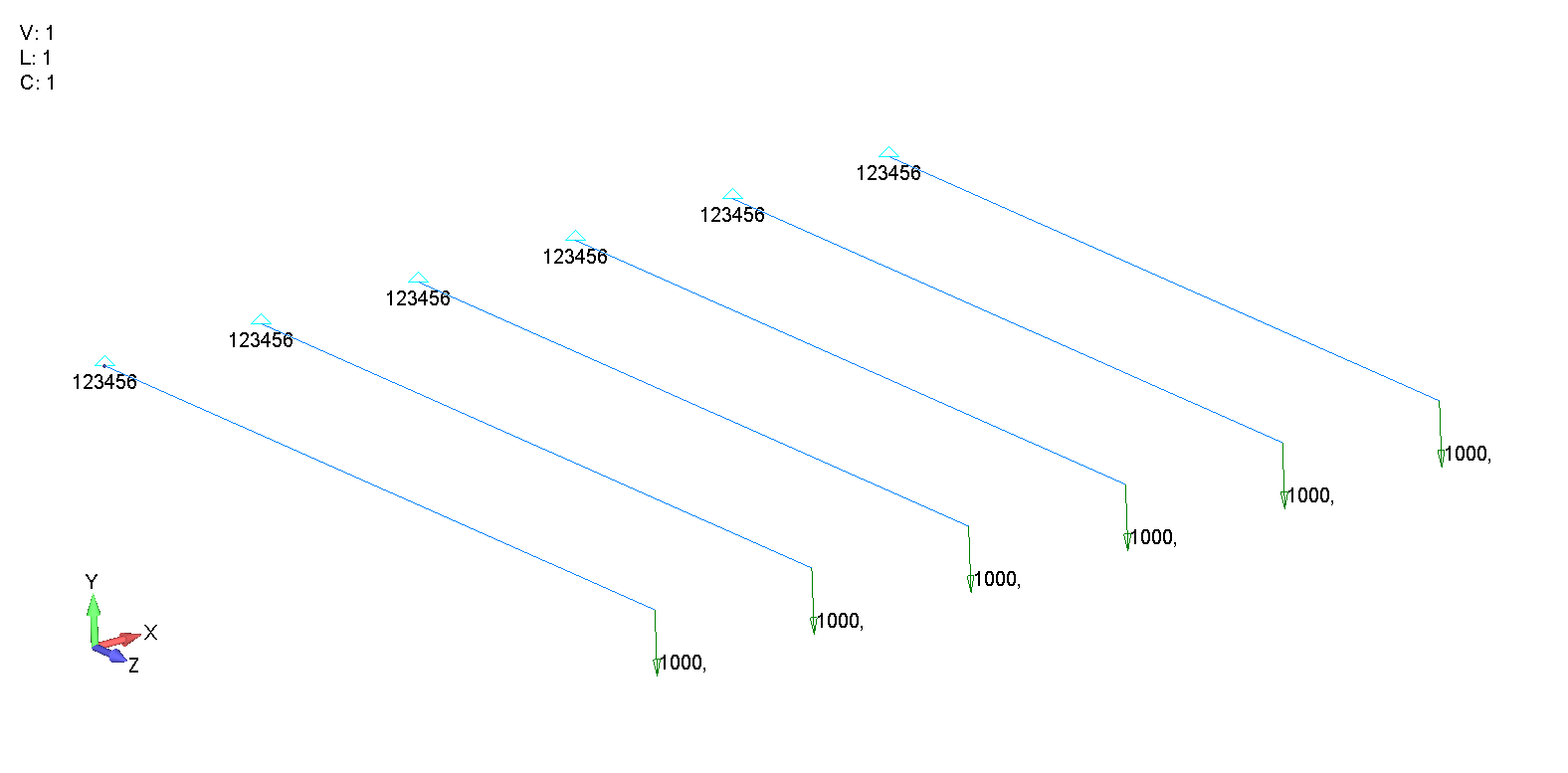
Obr. 4 Definice okrajových podmínek na nosnících tvořených nosníkovými elementy

Na obr.4 jsou zobrazena posunutí na jednotlivých nosnících, ze kterých je vidět, že počet elementů má velký vliv na tvar ohybu po délce nosníku. Nosník, který je tvořen pouze jedním elementem se žádným způsobem neohýbá, jeho volný konec se pouze posune ve směru působící síly. Čím více elementy je nosník tvořen tím pravidelnější je tvar ohybu. K největšímu ohybu dochází na volném konci nosníku a v tomto případě počet elementů nemá na výsledek vliv, u všech modelů je největší hodnota posunutí volného konce nosníku ve směru osy y - 2,0219 mm. Rozdílné hodnoty bychom zjistili např. v polovině nebo čtvrtině délky nosníku.

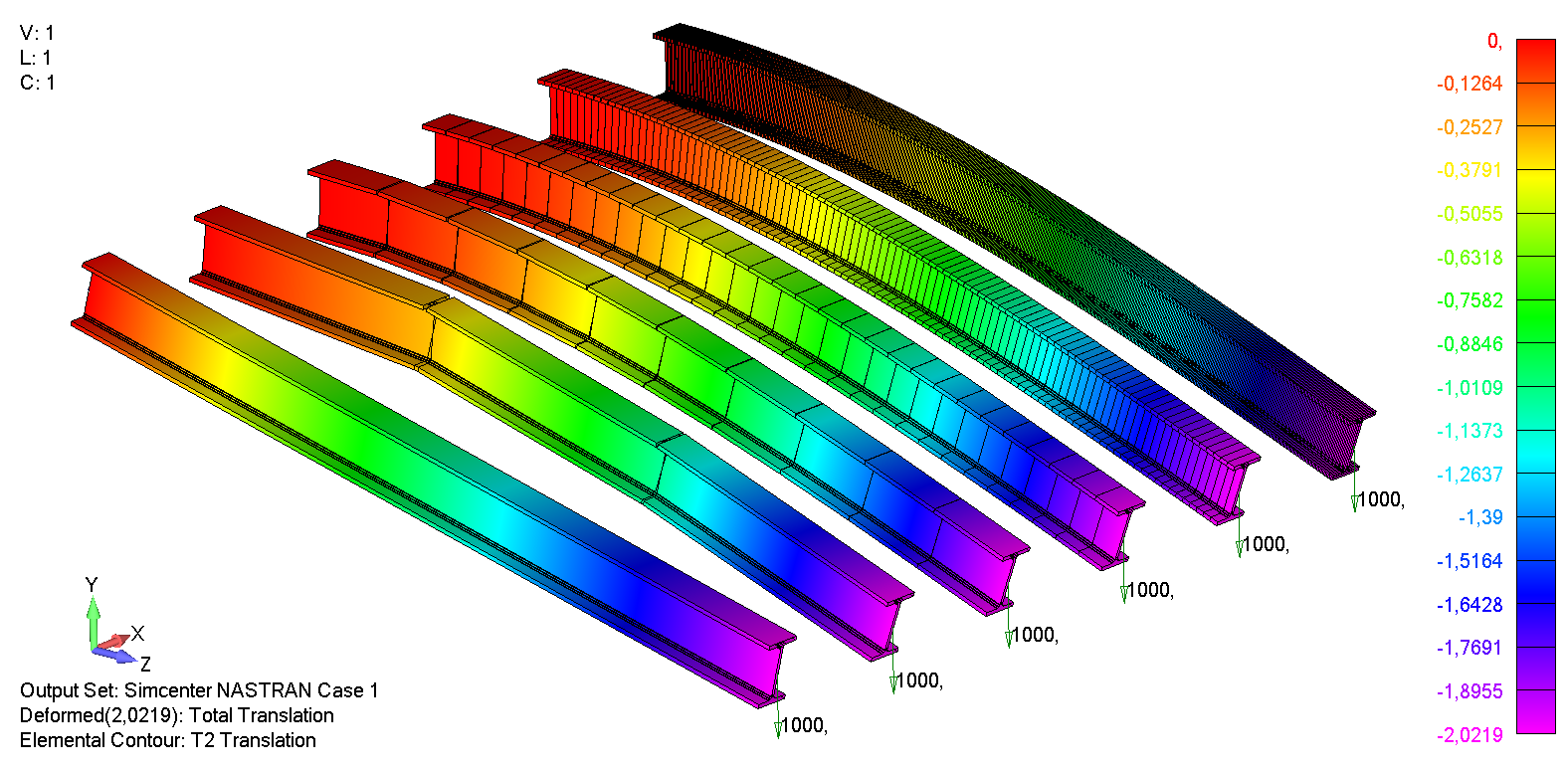
Obr. 5 Výsledná posunutí nosníku tvořeného nosníkovými elementy s různým počtem elementů

Na obr.5 jsou zobrazena natočení volného konce nosníků. Natočení na volných koncích jsou u všech elementů stejná a to φL=0,002969=0,17°.

Obr. 6 Výsledná natočení nosníků tvořených nosníkovými elementy s různým počtem elementů

V dalším pokračování bude ukázka výpočtu pomocí 2D skořepinových elementů, u kterých se již výsledky posunutí a natočení volného konce nosníku budou lišit.